Training neural networks with both convolutional and recurrent layers end-to-end provides a nice framework to model many problems. The general framework is as follows: given a series of images, automatically learn features, model temporal patterns, and output a vector (or value) at every timestep that represents something about each image. This has a ton of very interesting applications.
My main (longer term) motivation for exploring this is a larger project working towards automatic video summarization, using neural nets to extract scene information and figure out the frame-by-frame importance.
Anyway, as a starting point, I wanted to try a bunch of smaller models that allowed this type of end-to-end optimization. One very easy one to both understand and train is passing in a series of 1..N MNIST digits and calculating the sum of all the digit values added up.
Problem
For a given sequence of images like the following:


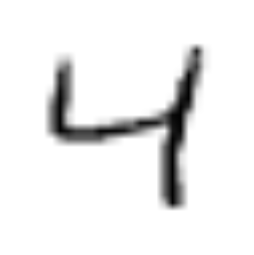

We want to train a neural network to calculate the sum, which in this case is 10 (I can add!).
Model Creation
To create our model, I used Keras, which is a very easy to use neural network library that runs on top of either Theano or Tensorflow. In particular, I use the Time Distributed Branch which is still under development, but I found stable enough to use.
Here’s our model:
model = Sequential()
model.add(TimeDistributed(Convolution2D(8, 4, 4,
border_mode='valid', activation='tanh'),
input_shape=(max_to_add, 1, img_rows, img_cols)))
model.add(TimeDistributed(Convolution2D(16, 3, 3,
border_mode='valid', activation='tanh')))
model.add(TimeDistributed(Flatten()))
model.add(GRU(output_dim=200, return_sequences=True))
model.add(GRU(output_dim=100, return_sequences=False))
model.add(Dropout(0.2))
model.add(Dense(1))
# Then compile the model with MSE and RMSProp
model.compile(loss='mean_squared_error', optimizer='rmsprop')
The goal here is to experiment with time distributed convolutions and feeding that into a RNN, not to make the best MNIST summation tool. As a result, the model parameters here are somewhat arbitrary and definitely suboptimal. Something interesting to note is that using relu activations caused numeric instability, with the loss getting immediately stuck at infinity. Tanh did not have this problem.
The key is that each layer in Keras has a TimeDistributed Wrapper around it, which basically applies that operation (in this case Convolution2D or Flatten) to all steps in the stack (so all images). This continues to happen until our TimeDistributed(Flatten()) which essentially flattens all the features out into a big matrix, and is fed into our RNN with GRU units.
Overall, the model works pretty well. With our max_to_add being set to 4, after 20 epochs our MSE on an evaluation set is 0.61, which is fairly small considering it is adding up to four digits from 0-9, meaning the result could be anywhere from 0 to 36.
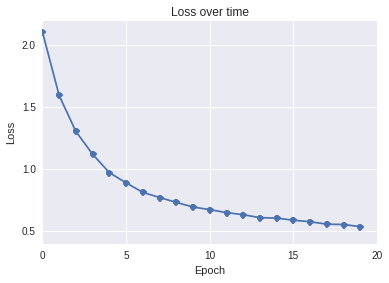
Visualizing Layer 1
The first layer consists of 8 4x4 weight matricies that are convolved with the image. What I really wanted to see is whether our convolution layers in our CNN->RNN model learn similar feature extractors to a similar model that uses softmax to predict a MNIST digit’s value.
Simple CNN
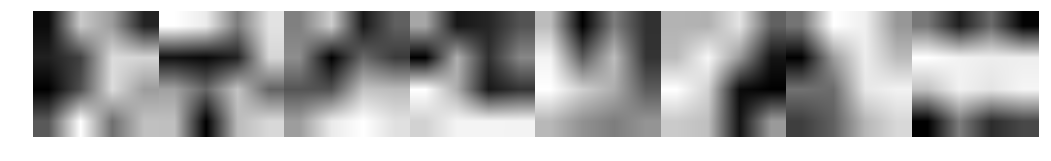
CNN-RNN
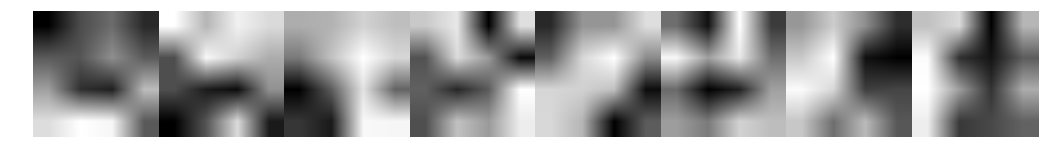
Further Work
An interesting follow on I have also played with is switching out the operation the RNN has to model. So for example changing addition to multiplication, and seeing how it responds. Initial tests seem to show that it takes much, much longer to converge to a decent loss, and seems to have trouble with large results (it can get 1x9 every time, but never gets 9x9). I want to explore model complexity and alternative loss functions to tease out what is causing the limitations there.
